Kumpulan Soal Matematika dan Pembahasannya Untuk Kelas IX SMP
Halo Sobat kelasmat, dalam kesempatan yang baik ini, saya ingin membagikan sebuah catatan mengenai kumpulan soal-soal matematika dan pembahasannya. Seperti biasa, sebelum memulai latihan soal, kelasmat ingin berbagi cerita terlebih dahulu mengenai salah satu konsep/materi matematika.
 Dan dalam kesempatan ini, kelasmat akan membahas tentang konsep perbandingan. Jadi silahkan dibaca-baca dulu ya. Namun, jika sobat kelasmat sudah tidak sabar ingin mengerjakan kumpulan soal yang saya bagikan dibawah ini, silahkan saja sobat lewati materi perbandingan ini.
Dan dalam kesempatan ini, kelasmat akan membahas tentang konsep perbandingan. Jadi silahkan dibaca-baca dulu ya. Namun, jika sobat kelasmat sudah tidak sabar ingin mengerjakan kumpulan soal yang saya bagikan dibawah ini, silahkan saja sobat lewati materi perbandingan ini.
Perbandingan sendiri terdiri dari dua jenis, yakni perbandingan senilai dan perbandingan berbalik nilai.
Untuk rumus perbandingan sendiri, antara rumus antara ke dua jenis tersebut berbeda. Sehingga soal perbandingan dan juga pengerjaannya juga berbeda. Jika kita lebih mendalami serta memahami materi ini, maka akan sangat bermanfaat dalam kehidupan kita sehari hari. Karena meskipun perbandingan ini tampak sepele, namun perbandingan memiliki fungsi yang besar dalam perkembangan matematika loh.
Sebagai contoh:
Nilai ujian matematika Dika adalah 80 dan nilai ujian matematika Laras 60. Nah, dari keterangan tersebut, maka bisa kita bandingkan data yang ada tadi menjadi:
1. Nilai ujian Dika 20 poin lebih besar dibandingkan nilai Laras. [Hal ini diperoleh dari perhitungan: 80 – 60 = 20 poin]
2. Nilai Dika empat per tiga kali lebih besar daripada nilai Laras. [Hal ini diperoleh dari perhitungan 80/60 = 4/3] Nah untuk melatih pemahaman kamu tentang matematika, silahkan coba jawab beberapa soal matematika dibawah ini ya...
Jika a = –15, b = 20 dan c = –5, maka nilai dari a – c × b + a : c adalah....
A. – 220
B. – 70
C. 88
D. 140
Jawaban: D
Pembahasan:
Jelas bahwa a – c × b + a : c
= (– 15) – (–5) × 20 + (– 15) : (– 5)
= (– 15) – (–100) + (3)
= – 15 + 100 + 3
= 88.
Pak Kamal mempunyai persediaan makanan ternak untuk 36 ekor sapi selama 8 hari. Agar persediaan makanan ternak pak Kamal mampu bertahan selama 24 hari, banyaknya jumlah sapi yang harus dijual pak Kamal adalah ... .
A. 108 buah
B. 24 buah
C. 12 buah
D. 10 buah
Jawaban: B
Pembahasan:
Diketahui : 36 ekor sapi mampu menghabis-kan persediaan makanan selama 8 hari Jika x ekor sapi mampu menghabiskan makanan selama 24 hari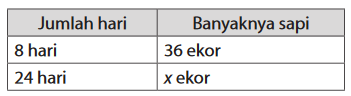
Dengan menggunakan perbandingan berbalik nilai diperoleh sebagai berikut!
\[\begin{array}{l} \Leftrightarrow \frac{8}{{24}} = \frac{x}{{36}}\\ \Leftrightarrow x = \frac{{36 \times 8}}{{24}}\\ \Leftrightarrow x = 12 \end{array}\]
Jadi, banyaknya sapi yang harus dipelihara pak Kamal adalah sebanyak 12 ekor. Sedangkan jumlah sapi yang harus dijual pak Kamal adalah 36 ekor – 12 ekor = 24 ekor.
Hasil dari \({343^{\frac{2}{3}}}\) adalah ... .
A. 7
B. 14
C. 42
D. 49
Jawaban: D
Pembahasan:
\[{343^{\frac{2}{3}}} = {\left( {{7^3}} \right)^{\frac{2}{3}}} = {7^{3 \times \frac{2}{3}}} = {7^2} = 49\]
Seorang pedagang alat membeli 20 lusin pensil seharga Rp140.000,-. Pedagang tersebut menjual kembali 10 lusin pensilnya dengan harga Rp10.000,-/lusin dan sisa pensilnya dijual seharga Rp 500/buah. Jika seluruh pensil pedangan tersebut terjual habis, maka keuntungan yang diperolehnya adalah ... .
A. Rp 18.000
B. Rp 20.000
C. Rp 25.000
D. Rp 40.000
Jawaban: B
Pembahasan:
Penjual pertama :
Harga jual pensil = 10 lusin × Rp10.000 = Rp100.000,-
Penjual kedua : Harga jual pensil = 10 lusin × 12 × Rp500 = Rp60.000,
Jadi jumlah uang yang diterima pedangan tersebut dari hasil penjualan pensilnya adalah = Rp100.000 + Rp60.000 = Rp160.000
Keuntungan yang diperoleh pedangang adalah = Rp160.000 – Rp140.000 = Rp20.000.
Perhatikan gambar persegi panjang ABCD dan persegi panjang AEFH berikut ini.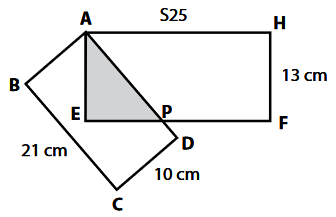
Diketahui panjang AB = 10 cm, BC = 21 cm, FH = 13 cm, dan AH = 25 cm. Selisih daerah bersih pada persegi panjang AEFH dengan daerah bersih pada persegi panjang ABCD adalah ...
A. \(102c{m^2}\)
A. \(115c{m^2}\)
A. \(124c{m^2}\)
A. \(142c{m^2}\)
Jawaban: B
Pembahasan:
Diketahui gambar persegi panjang ABCD dan persegi panjang AEFH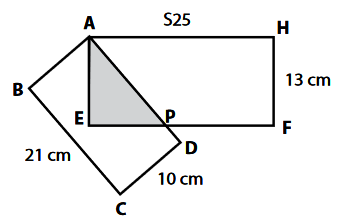
Perhatikan gambar persegi panjang ABCD.
Luas persegi panjang ABCD = 21 cm × 10 cm = 210 cm2
⇔ Luas ABCDE + Luas AEP = 210 cm2.........(1)
Perhatikan gambar persegi panjang AEFH.
Luas persegi panjang AEFH = 25 cm × 13 cm = 325 cm
⇔ Luas APFH + Luas AEP = 325 cm2.............(2)
Dari persamaan (1) dan (2) kita eliminasi maka diperoleh :
 Jadi Selisih daerah bersih pada persegi panjang AEFH dengan daerah bersih pada persegi panjang ABCD adalah 115 cm2
Jadi Selisih daerah bersih pada persegi panjang AEFH dengan daerah bersih pada persegi panjang ABCD adalah 115 cm2
Jawaban : C
Pembahasan:
Diketahui : perbandingan uang Agus : uang Puguh = 5 : 4 atau dapat juga dituliskan 15 : 12
perbandingan uang Bondan : uang Warno = 3 : 4 atau dapat dituliskan 12 : 16
Diperoleh perbandingan uang Agus : uang Puguh : uang Warno yaitu 15 : 12 : 16.
Jadi selisih uang Agus dan Warno adalah \(\frac{{16 - 15}}{{15 + 12 + 16}} \times Rp43.000 = Rp1.000\)
Untuk sementara, itu dulu ya kumpulan soal matematika kelas 9 nya. Nanti kalau ada waktu lagi, saya update postingan ini.

Sekilas tentang Perbandingan untuk SMP
Perbandingan merupakan suatu usaha yang kita lakukan untuk membandingkan antara dua hal atau lebih, baik itu dalam bentuk jumlah kuantitas maupun dalam bentuk ukuran. Perbandingan tersebut sebenarnya merupakan nilai pecahan yang disederhanakan. Sehingga, nilai dari suatu perbandingan bisa juga kita ibaratkan sebagai a dan b ataupun x dan y.Perbandingan sendiri terdiri dari dua jenis, yakni perbandingan senilai dan perbandingan berbalik nilai.
Untuk rumus perbandingan sendiri, antara rumus antara ke dua jenis tersebut berbeda. Sehingga soal perbandingan dan juga pengerjaannya juga berbeda. Jika kita lebih mendalami serta memahami materi ini, maka akan sangat bermanfaat dalam kehidupan kita sehari hari. Karena meskipun perbandingan ini tampak sepele, namun perbandingan memiliki fungsi yang besar dalam perkembangan matematika loh.
Sebagai contoh:
Nilai ujian matematika Dika adalah 80 dan nilai ujian matematika Laras 60. Nah, dari keterangan tersebut, maka bisa kita bandingkan data yang ada tadi menjadi:
1. Nilai ujian Dika 20 poin lebih besar dibandingkan nilai Laras. [Hal ini diperoleh dari perhitungan: 80 – 60 = 20 poin]
2. Nilai Dika empat per tiga kali lebih besar daripada nilai Laras. [Hal ini diperoleh dari perhitungan 80/60 = 4/3] Nah untuk melatih pemahaman kamu tentang matematika, silahkan coba jawab beberapa soal matematika dibawah ini ya...
Kumpulan Soal Matematika SMP kelas 9 dan Pembahasannya
Soal 1
Jika a = –15, b = 20 dan c = –5, maka nilai dari a – c × b + a : c adalah....
A. – 220
B. – 70
C. 88
D. 140
Pembahasan soal 1
Jawaban: D
Pembahasan:
Jelas bahwa a – c × b + a : c
= (– 15) – (–5) × 20 + (– 15) : (– 5)
= (– 15) – (–100) + (3)
= – 15 + 100 + 3
= 88.
Soal 2
Pak Kamal mempunyai persediaan makanan ternak untuk 36 ekor sapi selama 8 hari. Agar persediaan makanan ternak pak Kamal mampu bertahan selama 24 hari, banyaknya jumlah sapi yang harus dijual pak Kamal adalah ... .
A. 108 buah
B. 24 buah
C. 12 buah
D. 10 buah
Pembahasan soal 2
Jawaban: B
Pembahasan:
Diketahui : 36 ekor sapi mampu menghabis-kan persediaan makanan selama 8 hari Jika x ekor sapi mampu menghabiskan makanan selama 24 hari

Dengan menggunakan perbandingan berbalik nilai diperoleh sebagai berikut!
\[\begin{array}{l} \Leftrightarrow \frac{8}{{24}} = \frac{x}{{36}}\\ \Leftrightarrow x = \frac{{36 \times 8}}{{24}}\\ \Leftrightarrow x = 12 \end{array}\]
Jadi, banyaknya sapi yang harus dipelihara pak Kamal adalah sebanyak 12 ekor. Sedangkan jumlah sapi yang harus dijual pak Kamal adalah 36 ekor – 12 ekor = 24 ekor.
Soal 3
Hasil dari \({343^{\frac{2}{3}}}\) adalah ... .
A. 7
B. 14
C. 42
D. 49
Pembahasan soal 3
Jawaban: D
Pembahasan:
\[{343^{\frac{2}{3}}} = {\left( {{7^3}} \right)^{\frac{2}{3}}} = {7^{3 \times \frac{2}{3}}} = {7^2} = 49\]
Soal 4
Seorang pedagang alat membeli 20 lusin pensil seharga Rp140.000,-. Pedagang tersebut menjual kembali 10 lusin pensilnya dengan harga Rp10.000,-/lusin dan sisa pensilnya dijual seharga Rp 500/buah. Jika seluruh pensil pedangan tersebut terjual habis, maka keuntungan yang diperolehnya adalah ... .
A. Rp 18.000
B. Rp 20.000
C. Rp 25.000
D. Rp 40.000
Pembahasan soal 4
Jawaban: B
Pembahasan:
Penjual pertama :
Harga jual pensil = 10 lusin × Rp10.000 = Rp100.000,-
Penjual kedua : Harga jual pensil = 10 lusin × 12 × Rp500 = Rp60.000,
Jadi jumlah uang yang diterima pedangan tersebut dari hasil penjualan pensilnya adalah = Rp100.000 + Rp60.000 = Rp160.000
Keuntungan yang diperoleh pedangang adalah = Rp160.000 – Rp140.000 = Rp20.000.
Soal 5
Perhatikan gambar persegi panjang ABCD dan persegi panjang AEFH berikut ini.

Diketahui panjang AB = 10 cm, BC = 21 cm, FH = 13 cm, dan AH = 25 cm. Selisih daerah bersih pada persegi panjang AEFH dengan daerah bersih pada persegi panjang ABCD adalah ...
A. \(102c{m^2}\)
A. \(115c{m^2}\)
A. \(124c{m^2}\)
A. \(142c{m^2}\)
Pembahasan Soal 5
Jawaban: B
Pembahasan:
Diketahui gambar persegi panjang ABCD dan persegi panjang AEFH

Perhatikan gambar persegi panjang ABCD.
Luas persegi panjang ABCD = 21 cm × 10 cm = 210 cm2
⇔ Luas ABCDE + Luas AEP = 210 cm2.........(1)
Perhatikan gambar persegi panjang AEFH.
Luas persegi panjang AEFH = 25 cm × 13 cm = 325 cm
⇔ Luas APFH + Luas AEP = 325 cm2.............(2)
Dari persamaan (1) dan (2) kita eliminasi maka diperoleh :

Soal 6
Diketahui perbandingan uang Agus dan Uang Puguh adalah 5 : 4 dan perbandingan uang Puguh dan uang Warno = 3 : 4. Jika jumlah uang Agus, Puguh, dan Warno Rp43.000. Selisih uang Agus dan Warno adalah ... .Pembahasan SOal 6
Jawaban : C
Pembahasan:
Diketahui : perbandingan uang Agus : uang Puguh = 5 : 4 atau dapat juga dituliskan 15 : 12
perbandingan uang Bondan : uang Warno = 3 : 4 atau dapat dituliskan 12 : 16
Diperoleh perbandingan uang Agus : uang Puguh : uang Warno yaitu 15 : 12 : 16.
Jadi selisih uang Agus dan Warno adalah \(\frac{{16 - 15}}{{15 + 12 + 16}} \times Rp43.000 = Rp1.000\)
Untuk sementara, itu dulu ya kumpulan soal matematika kelas 9 nya. Nanti kalau ada waktu lagi, saya update postingan ini.





