Penerapan Himpunan dalam Pemecahan Masalah Sehari-hari

Melanjutkan tulisan saya yang kemarin mengenai memahami konsep himpunan dengan mudah, maka kali ini saatnya menerapkan konsep himpunan tersebut dalam pemecahan masalah sehari-hari. Namun sebelum itu, mari kita pahami terlebih dulu bagaimana menyajikan himpunan kedalam diagram venn sehingga nanti akan libih terbantu dalam pemeceahan masalah yang akan kita lakukan.

Menyajikan Himpunan dengan Diagram Venn dan Penerapannya dalam Pemecahan Masalah Sehari-hari

Masalah Kontekstual

Untuk memudahkan pemecahan masalah, himpunan-himpunan yang ada dapat disajikan dalam bentuk diagram Venn. Dengan cara penyajian tersebut, menjadi lebih mudah bagi kita dalam membayangkan cara pemecahannya. Selain itu, kita juga dapat mengetahui lebih lanjut tentang hubungan (relasi) yang dapat terjadi antara himpunan-himpunan tersebut.

Apa itu Social Engineering dan Cara Menghadapinya

Social Engineering adalah Sebuah Teknik untuk Memanipulasi dan Mengarahkan Perilaku Seseorang atau Sekelompok Orang dengan Menggunakan Kekuatan Hipnotik Bahasa, Rasa Rikuh atau ragu serta Preferensi Pribadi Seseorang Terhadap Suatu Isu.

Kelasmat.comArRahim

Aturan Diagram Venn

Pada penyajian himpunan menggunakan diagram Venn, himpunan semesta umumnya digambarkan menggunakan lambang persegi panjang. Sementara himpunan-himpunan bagian yang ada di dalamnya digambarkan menggunakan bentuk lingkaran atau elips. Tujuannya adalah untuk memudahkan dalam memahami himpunan dan hubungan (relasi) antara himpunan yang satu dengan himpunan lainnya.

Operasi Biner

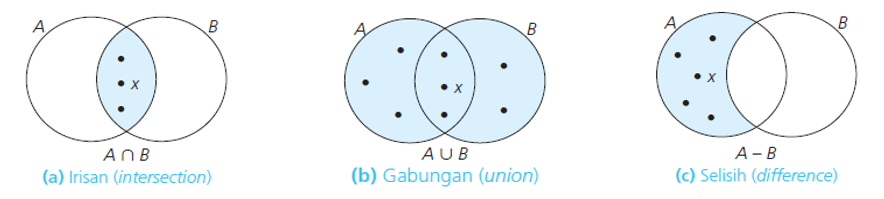
Operasi biner adalah operasi yang dilakukan antara dua unsur sehingga dihasilkan unsur tunggal. Pada himpunan, operasi biner yang dimaksud terdiri dari irisan (intersection), gabungan (union), selisih (difference), dan perkalian (multiplication). Sementara operasi uner adalah operasi yang dilakukan terhadap sebuah unsur sehingga dihasilkan unsur tunggal.

Baca Juga : Soal Ulangan Harian Pola Bilangan Kelas 8{alertWarning}

Contoh Soal

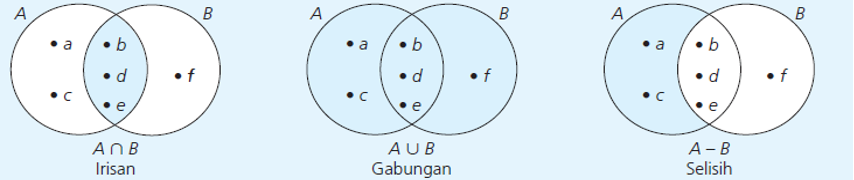
Diketahui A = {a, b, c, d, e} dan B = {b, d, e, f }. Gambarkan diagram Venn dari kedua himpunan tersebut, kemudian tentukan himpunan-himpunan A ∩ B, A ∪ B, dan A – B. Gambarkan juga diagram Venn dari setiap himpunan tersebut.

Jawab:
Perhatikan bahwa himpunan A = {a, b, c, d, e} dan B = {b, d, e, f} saling beririsan.
Irisannya adalah {b, d, e}, sehingga diagram Venn dari himpunan A dan B berpotongan.
Dengan demikian, setiap diagram Venn dari himpunan A ∩ B, A ∪ B, dan A – B adalah sebagai berikut.

Berdasarkan diagram Venn tersebut, hasil operasi biner dari himpunan A dan B adalah:
A ∩ B = {b, d, e},
A ∪ B = {a, b, c, d, e, f }, dan
A – B = {a, c}.{alertSuccess}

Operasi Uner

Pada himpunan, satu-satunya operasi yang berupa operasi uner adalah operasi komplemen (ingkaran) dari suatu himpunan. Komplemen dari himpunan A adalah himpunan yang semua elemennya anggota S tetapi bukan anggota A, ditulis dengan lambang A^c atau A’.

Contoh Soal

Diketahui semesta S = {1, 2, 3, 4, 5, 6, 7, 8, 9}. A dan B adalah himpunan-himpunan dalam semesta S dengan A = {1, 2, 3, 4, 5} dan B = {2, 4, 6, 7}. Gambarkan diagram Venn yang memperlihatkan hubungan antara ketiga himpunan S, A, dan B. Berdasarkan diagram Venn tersebut, tuliskan dengan cara mendaftar himpunan setiap irisan, gabungan, dan selisih.

Jawab:
Himpunan A = {a, b, c, d, e} dan B = {b, d, e, f} saling beririsan.
Irisannya adalah {b, d, e}, sehingga diagram Venn dari himpunan A dan B berpotongan.
Dengan demikian, setiap diagram Venn dari himpunan A ∩ B, A ∪ B, dan A – B adalah sebagai berikut.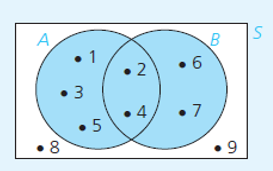

Diagram Venn yang memperlihatkan hubungan antara ketiga himpunan S, A, dan B tersebut adalah
{alertSuccess}

Pemecahan Masalah Menggunakan Himpunan

Untuk setiap dua himpunan A dan B, berlaku:

Rumus di atas dikenal sebagai rumus umum banyak anggota dua himpunan. Rumus tersebut berlaku secara umum, artinya berlaku untuk semua relasi antara dua himpunan. Dengan menggunakan rumus tersebut memungkinkan kita untuk menjawab masalah kontekstual yang diberikan di awal tentang penerapan himpunan dalam pemecahan masalah

Cara Mengatasi Serangan Trojan

Sedikitnya ada 7 cara yang bisa kita lakukan dalam mengatasi serangan virus Trojan. Apa saja cara itu?, silahkan simak penjelasan singkat berikut ini.

Kelasmat.comArRahim

Contoh Soal

Pada sebuah wilayah RT (Rukun Tetangga) yang terdiri dari 16 KK (Kepala Keluarga) terdapat 10 KK yang memiliki sepeda motor, 6 KK memiliki mobil, dan 3 KK tidak memiliki sepeda motor maupun mobil. Masalah yang ditanyakan adalah berapa KK yang memiliki mobil sekaligus memiliki sepeda motor?

Jawab:
S = himpunan seluruh KK, maka n(S) = 16,
A = himpunan KK pemilik sepeda motor, maka n(A) = 10,
dan B = himpunan KK pemilik mobil, maka n(B) = 6.
Sebanyak 3 KK tidak memiliki sepeda motor maupun mobil, maka yang dimaksud adalah:
n(A ∪ B)c = 3.
Karena n(A ∪ B)^c = 3,
maka n(A ∪ B) = n(S) – n(A ∪ B)^c = 16 – 3 = 13
Misalkan n(A ∩ B) = x,
maka:
n(A ∪ B) = n(A) + n(B) – n(A ∩ B)
13 = 10 + 6 – x
x = 10 + 6 – 13 = 3
Jadi, banyaknya KK yang memiliki sepeda motor dan mobil ada 3 KK.
{alertSuccess}